EXPONENTIAL MEANING: KIẾN THỨC VỀ SỐ MŨ TRONG TOÁN TIẾNG ANH

 

Đối với môn toán tiếng Anh, khái niệm "exponential meaning" đóng vai trò quan trọng và phổ biến. Tuy nhiên, nhiều học sinh vẫn không khỏi băn khoăn khi gặp phải chủ đề này trong bài thi. Vậy thì hôm nay, hãy cùng Happymath giải đáp các thắc mắc về “exponential meaning” và cách giải quyết các bài toán liên quan nhé.

Exponential là gì

Exponential là một loại hàm số toán học, thường được biểu diễn dưới dạng f(x) = a^x, trong đó "x" là biến số và "a" là hằng số gọi là cơ số của hàm số và phải lớn hơn 0. Cơ số thường được sử dụng phổ biến nhất cho hàm số mũ trong toán học là số transcendental "e," gần giống với 2.71828.

Exponential meaning được xem liên quan đến tốc độ tăng cấp số nhân, nghĩa là khi giá trị tăng một cách nhanh chóng theo một mức độ không đổi. Số mũ và các hàm số mũ có ứng dụng rộng rãi trong khoa học, kỹ thuật, tài chính, và nhiều lĩnh vực khác để mô tả sự tăng trưởng và thay đổi theo thời gian.

Exponential Functions là gì

Công thức của hàm số mũ

Công thức của hàm số mũ trong toán học được định nghĩa bởi f(x) = a^x, trong đó biến x xuất hiện như một số mũ. Bạn cần lưu ý rằng toán số mũ phụ thuộc vào số mũ và giá trị của biến x.

Hàm số mũ có dạng f(x) = a^x, trong đó a > 0 và a 1. Biến x có thể là bất kỳ số thực nào.

Nếu biến x là số âm, thì hàm số này không xác định (undefined) trong khoảng -1 < x < 1.

Trong công thức này:

• "x" là biến số.

• "a" là một hằng số gọi là cơ số của hàm số.

Hàm số mũ biểu thị sự tăng trưởng hoặc suy giảm dựa trên công thức này. Bất kỳ đại lượng nào tăng hoặc giảm một phần trăm cố định sau các khoảng thời gian đều thể hiện sự tăng trưởng hoặc suy giảm theo hình thức số mũ.

Tăng trưởng theo số mũ

Trong trường hợp này, đại lượng tăng chậm ban đầu, sau đó tăng nhanh chóng. Tốc độ tăng trưởng tăng theo thời gian. Tốc độ tăng trưởng trở nên nhanh hơn khi thời gian trôi qua. Sự tăng trưởng nhanh chóng này được gọi là "sự tăng trưởng số mũ". Công thức để định nghĩa tăng trưởng số mũ là: y = a(1 + r)^x, với r là tỷ lệ tăng trưởng.

Suy giảm theo số mũ

Lúc này, đại lượng giảm mạnh ban đầu, sau đó giảm chậm. Tốc độ giảm giảm theo thời gian. Tốc độ giảm trở nên chậm hơn khi thời gian trôi qua. Sự giảm mạnh ban đầu này được gọi là "sự giảm số mũ". Công thức để định nghĩa suy giảm số mũ là: y = a(1 - r)^x, với r là tỷ lệ suy giảm.

Đồ thị hàm số mũ

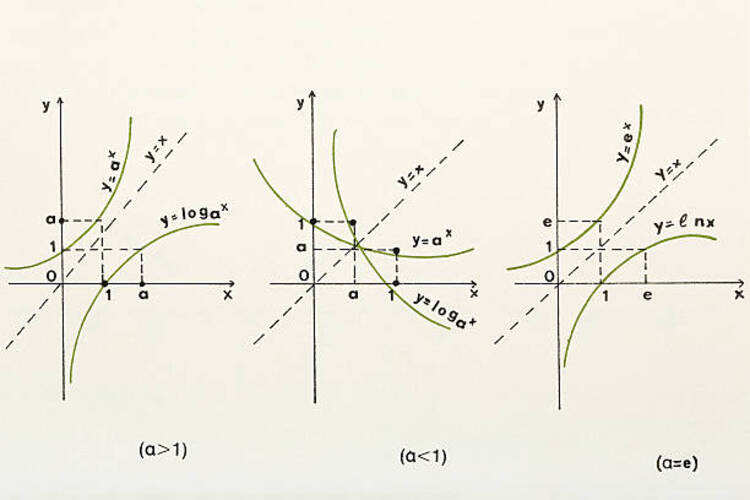
Đồ thị của hàm số mũ f(x) = a^x phụ thuộc vào giá trị của cơ số "a". Trong đó:

• a > 1: Đồ thị tăng dần và tiệm cận đến trục x (đường y = 0) khi x tiến về vô cùng. Ví dụ, đồ thị của hàm số mũ với a = 2 sẽ là một đường cong tăng dần.

• 0 < a < 1: Đồ thị giảm dần và tiệm cận đến trục x khi x tiến về vô cùng. Ví dụ, đồ thị của hàm số mũ với a = 1/2 sẽ là một đường cong giảm dần.

• a = 1: Đồ thị là một đường ngang tại y = 1. Không có sự tăng hoặc giảm khi x thay đổi.

• a < 0: Đồ thị không xác định trong ngữ cảnh của hàm số mũ. Chúng ta thường chỉ cần xem xét hàm số mũ với cơ số dương.

Bên dưới là ví dụ về đồ thị của hàm số mũ với cơ số "a" khác nhau:

• Đồ thị của f(x) = 2^x sẽ là một đường cong tăng dần.

• Đồ thị của f(x) = (1/2)^x sẽ là một đường cong giảm dần.

• Đồ thị của f(x) = 1^x (hoặc bất kỳ số thực dương nào) sẽ là một đường ngang tại y = 1.

Đạo hàm hàm số mũ

Đạo hàm của hàm số e^x theo biến x chính là chính nó, tức là d(e^x)/dx = e^x.

Lưu ý, hàm số mũ f(x) = e^x có một đặc tính đặc biệt. Đạo hàm của hàm số này chính là hàm số này bản thân nó. Tức là f'(x) = e^x = f(x).

Trong thuật ngữ toán học, điều này thể hiện một tính chất độc đáo của hàm số mũ, nghĩa là đạo hàm của nó luôn bằng chính nó.

Giải toán số mũ

Bài toán: Đơn giản hóa hàm số mũ: 2^x - 2^(x+1)

Ta có:

Hàm số mũ cho trước: 2^x - 2^(x+1)

Bằng cách sử dụng tính chất: a^x * a^y = a^(x+y)

Do đó, 2^(x+1) có thể được viết lại dưới dạng 2^x * 2

Như vậy, hàm số cho trước có thể được viết lại như sau:

2^x - 2^(x+1) = 2^x - 2^x * 2

Bây giờ, chúng ta sẽ phân tách thành phần 2x:

2^x - 2^(x+1) = 2^x - 2^x * 2 = 2^(x(1 - 2))

2^x - 2^(x+1) = 2^(x(-1))

2^x - 2^(x+1) = -2^x

Quy tắc của toán số mũ

a^x * a^ = a^(x+y): Nhân hai số mũ có cùng cơ số a mà có số mũ khác nhau (x và y), thì kết quả là số mũ có cùng cơ số a và số mũ là tổng của x và y.

• a^x / a^y = a^(x-y): Chia hai số mũ có cùng cơ số a mà có số mũ khác nhau (x và y), thì kết quả là số mũ có cùng cơ số a và số mũ là hiệu của x và y.

• (a^x)^y = a^(xy): Khi lấy số mũ của một số mũ, thì kết quả là số mũ với cùng cơ số a và số mũ bằng tích của x và y.

• a^x * b^x = (ab)^x: Nhân hai số mũ có cùng số mũ x nhưng cơ số khác nhau (a và b), thì kết quả là số mũ với cùng số mũ x và cơ số là tích của a và b.

• (a/b)^x = a^x / b^x: Khi lấy số mũ của một phân số (a/b) với số mũ x, thì kết quả là phân số với cùng số mũ x, và cơ số của tử số là số mũ của a và mẫu số là số mũ của b.

• a^0 = 1: Bất kỳ số mũ nào được đưa lên số 0 đều bằng 1. 

• a^(-x) = 1 / (a^x): Khi bạn có số mũ âm (-x), kết quả là nghịch đảo của số mũ dương (a^x). Như vậy, các số mũ có thể được biểu diễn dưới dạng phân số với số mũ âm.

Tổng kết

Vậy là chúng ta đã khám phá "exponential meaning," một khái niệm quan trọng trong toán học và học toán tiếng Anh. Nắm vững kiến thức về "exponential meaning" sẽ giúp bạn xây dựng nền tảng mạnh mẽ cho sự hiểu biết và ứng dụng trong thực tế. Hy vọng những thông tin mà Happy Math chia sẻ sẽ đồng hành cùng bạn chinh phục môn toán dễ dàng hơn.